Junsoo Park

O(1) is holy

-Hamid Tizhoosh

1. Big-O Notation Primer

The Big-O notation measures the worst-case complexity of an algorithm. on O(n), n represents the number of inputs. It follows this question "What will happen as n approaches infinity?"

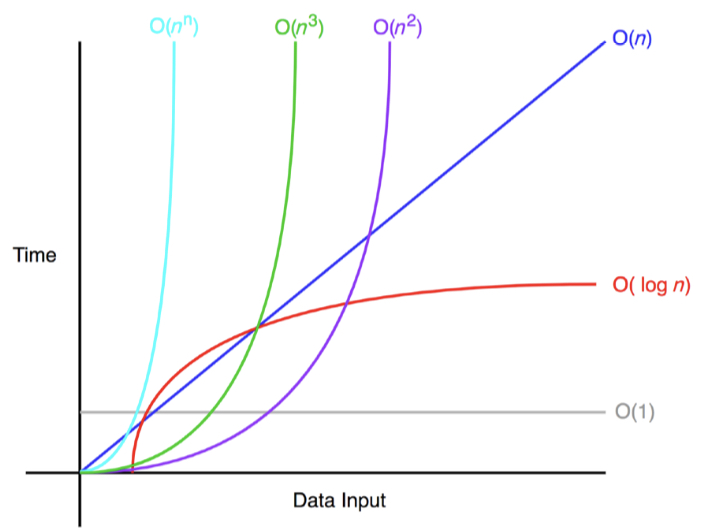
2. Common Examples

O(1) is holy. Even if you put tonnes of inputs in a function, which has O(1), the time of processing is always the same.

The efficiency of logarithmic time complexities is apparent with large inputs. For example, Although n is a million, exampleLogarithmic will print only 19 times because log(1000000) = 19.931...

3. Rules of Big-O Notation

• Coefficient rule: If f(n) is O(g(n)), then Kf(n), for any constant k>0. This rule eliminates coefficients not related to the input size n.
• Sum rule: if f(n) is O(h(n)) and g(n) is O(p(n)), then f(n) + g(n) is O(f(n) + g(n)).
• Product rule: if f(n) is O(h(n)) and g(n) is O(p(n)), then f(n) * g(n) is O(f(n) * g(n)).
• Transitive rule: if f(n) is O(g(n)) and g(n) is O(h(n)), then f(n) is O(h(n)).
• Polynomial rule: If f(n) is a polynomial of degree k, then f(n) is O(n^k).
• Log of a power rule: log(nk) is O(log(n) for any constant k>0. With the log of a power rule, constants within a log function are also ignored in Big-O notation.

4. Coefficient Rule: "Get Rid of Constants"

Let's first review the coefficient rule. f(n) is O(g(n)), then Kf(n), for any constant k>0.

This code block has f(n) = n because it adds to the count n times. Therefore, this function is O(n) in time complexity

This block has f(n) = 5n because it runs from 0 to 5n. However, this code block also has O(n). Simply put this is because if n is close to infinity or another large number, those four additional operations are meaningless.

Lastly, this code block has f(n) = n + 1. There is +1 from the last operation (count +=3). This still has a Big-O notation of O(n) because that 1 operation is not up to the input n. As n approaches infinity, it will become negligible.

5. Sum Rule: "Add Big-Os Up"

if f(n) is O(h(n)) and g(n) is O(p(n)), then f(n) + g(n) is O(f(n) + g(n)).

It is important to remember to apply the coefficient rule after applying this rule.

in this example, line 4 has f(n) = n and line 7 has f(n) = 5n. this results in 6n. However, when applying the coefficient rule, the final result is O(n) = n

6. Product Rule: "Multiply Big-Os"

if f(n) is O(h(n)) and g(n) is O(p(n)), then f(n) * g(n) is O(f(n) * g(n)).

The following code block demonstrates a function with two nested for loops for which the product rule is applied.

In this example, f(n) = 5n*n because line 7 runs 5n times for a total of n iterations. Therefore, this results in a total of 5n² operations. Applying the coefficient rule, the result is that O(n)=n²

7. Polynomial Rule: "Big-O to the Power of k"

If f(n) is a polynomial of degree k, then f(n) is O(n^k).

This "k" means the times of running loop

In this example, f(n) = n^2 because line 4 runs n*n iterations

8. Summary

Big-O is important for analyzing and comparing the efficiencies of algorithms. The analysis of Big-O Starts by looking at the code and applying the rules to simplify the Big-O notation. The following are the most often-used rules:

• Elimination coefficients/constants (coefficient rule)
• Adding up Big-Os (sum rule)
• Multiplying Big-Os (product rule)
• Determining the polynomial of the Big-O notation by looking at loops(polynomial rule)