
[Javascript Data Structure and Algorithms] Chapter1. Big-O Notation
O(1) is holy
-Hamid Tizhoosh
1. Big-O Notation Primer
The Big-O notation measures the worst-case complexity of an algorithm. on O(n), n represents the number of inputs. It follows this question "What will happen as n approaches infinity?"
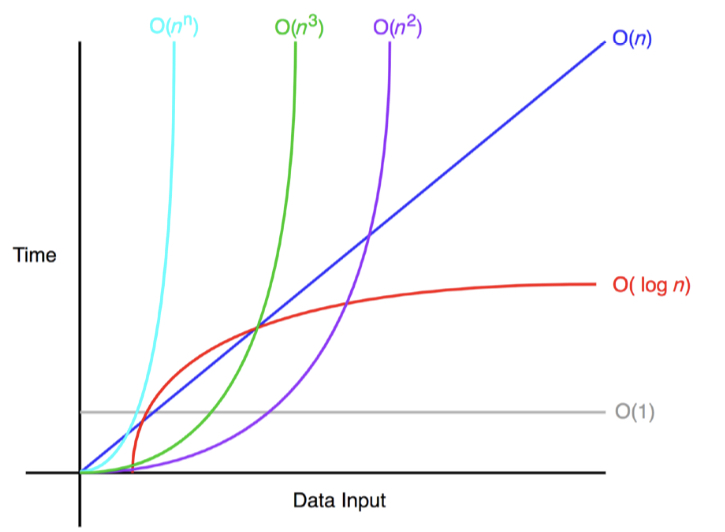
2. Common Examples
O(1) is holy. Even if you put tonnes of inputs in a function, which has O(1), the time of processing is always the same.
The efficiency of logarithmic time complexities is apparent with large inputs. For example, Although n is a million, exampleLogarithmic will print only 19 times because log(1000000) = 19.931...
3. Rules of Big-O Notation
- Coefficient rule: If f(n) is O(g(n)), then Kf(n), for any constant k>0. This rule eliminates coefficients not related to the input size n.
- Sum rule: if f(n) is O(h(n)) and g(n) is O(p(n)), then f(n) + g(n) is O(f(n) + g(n)).
- Product rule: if f(n) is O(h(n)) and g(n) is O(p(n)), then f(n) * g(n) is O(f(n) * g(n)).
- Transitive rule: if f(n) is O(g(n)) and g(n) is O(h(n)), then f(n) is O(h(n)).
- Polynomial rule: If f(n) is a polynomial of degree k, then f(n) is O(n^k).
- Log of a power rule: log(nk) is O(log(n) for any constant k>0. With the log of a power rule, constants within a log function are also ignored in Big-O notation.
4. Coefficient Rule: "Get Rid of Constants"
Let's first review the coefficient rule. f(n) is O(g(n)), then Kf(n), for any constant k>0.
This code block has f(n) = n because it adds to the count n times. Therefore, this function is O(n) in time complexity
This block has f(n) = 5n because it runs from 0 to 5n. However, this code block also has O(n). Simply put this is because if n is close to infinity or another large number, those four additional operations are meaningless.
Lastly, this code block has f(n) = n + 1. There is +1 from the last operation (count +=3). This still has a Big-O notation of O(n) because that 1 operation is not up to the input n. As n approaches infinity, it will become negligible.
5. Sum Rule: "Add Big-Os Up"
if f(n) is O(h(n)) and g(n) is O(p(n)), then f(n) + g(n) is O(f(n) + g(n)).
It is important to remember to apply the coefficient rule after applying this rule.
in this example, line 4 has f(n) = n and line 7 has f(n) = 5n. this results in 6n. However, when applying the coefficient rule, the final result is O(n) = n
6. Product Rule: "Multiply Big-Os"
if f(n) is O(h(n)) and g(n) is O(p(n)), then f(n) * g(n) is O(f(n) * g(n)).
The following code block demonstrates a function with two nested for loops for which the product rule is applied.
In this example, f(n) = 5n*n because line 7 runs 5n times for a total of n iterations. Therefore, this results in a total of 5n² operations. Applying the coefficient rule, the result is that O(n)=n²
7. Polynomial Rule: "Big-O to the Power of k"
If f(n) is a polynomial of degree k, then f(n) is O(n^k).
This "k" means the times of running loop
In this example, f(n) = n^2 because line 4 runs n*n iterations
8. Summary
Big-O is important for analyzing and comparing the efficiencies of algorithms. The analysis of Big-O Starts by looking at the code and applying the rules to simplify the Big-O notation. The following are the most often-used rules:
- Elimination coefficients/constants (coefficient rule)
- Adding up Big-Os (sum rule)
- Multiplying Big-Os (product rule)
- Determining the polynomial of the Big-O notation by looking at loops(polynomial rule)
